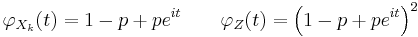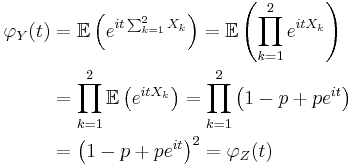Convolution of probability distributions
The convolution of probability distributions arises in probability theory and statistics as the operation in terms of probability distributions that corresponds to the addition of independent random variables and, by extension, to forming linear combinations of random variables. The operation here is a special case of convolution for which special results apply because the context is that of probability distributions.
Contents |
Introduction
The probability distribution of the sum of two or more independent random variables is the convolution of their individual distributions. The term is motivated by the fact that the probability mass function or probability density function of a sum of random variables is the convolution of their corresponding probability mass functions or probability density functions respectively. Many well known distributions have simple convolutions: see List of convolutions of probability distributions
Example derivation
There are several ways of derive formulae for the convolution of probability distributions. Often the manipulation of integrals can be avoided by use of some type of generating function. Such methods can also be useful in deriving properties of the resulting distribution, such as moments, even if an explicit formula for the distribution itself cannot be derived.
One of the straightforward techniques is to use characteristic functions, which always exists and are unique to a given distribution.
Convolution of Bernoulli distributions
The convolution of two independent Bernoulli random variables is a Binomial random variable. That is, in a shorthand notation,
To show this let
and define
Also, let Z denote a generic binomial random variable:
Using probability mass functions
As 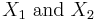 are independent,
are independent,
Here, use was made of the fact that 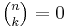 for k>n in the last but three equality, and of Pascal's rule in the second last equality.
for k>n in the last but three equality, and of Pascal's rule in the second last equality.
Using characteristic functions
The moment generating function of each 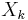 and of
and of 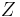 is
is
where t is within some neighborhood of zero.
The expectation of the product is the product of the expectations since each 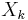 is independent. Since
is independent. Since  and
and 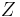 have the same characteristic function, they must have the same distribution.
have the same characteristic function, they must have the same distribution.
References
- Hogg, Robert V.; McKean, Joseph W.; Craig, Allen T. (2004). Introduction to mathematical statistics (6th ed.). Upper Saddle River, New Jersey: Prentice Hall. pp. 692. ISBN 9780130085078. MR467974. http://www.pearsonhighered.com/educator/product/Introduction-to-Mathematical-Statistics/9780130085078.page.
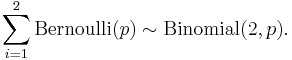
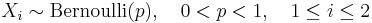
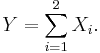
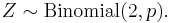
![\begin{align}\mathbb{P}[Y=n]&=\mathbb{P}\left[\sum_{i=1}^2 X_i=n\right] \\
&=\sum_{m\in\mathbb{Z}} \mathbb{P}[X_1=m]\times\mathbb{P}[X_2=n-m] \\
&=\sum_{m\in\mathbb{Z}}\left[\binom{1}{m}p^m\left(1-p\right)^{1-m}\right]\left[\binom{1}{n-m}p^{n-m}\left(1-p\right)^{1-n%2Bm}\right]\\
&=p^n\left(1-p\right)^{2-n}\sum_{m\in\mathbb{Z}}\binom{1}{m}\binom{1}{n-m} \\
&=p^n\left(1-p\right)^{2-n}\left[\binom{1}{n}\binom{1}{0}%2B\binom{1}{n-1}\binom{1}{1}\right]\\
&=\binom{2}{n}p^n\left(1-p\right)^{2-n}=\mathbb{P}[Z=n]
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/a18584a1b0b0fcb6aa94bbb1839f4b70.png)